One-dimensional Deterministic Greenberg--Hastings Models
Robert Fisch
Department of Computer Science,
University of Wisconsin,
Madison, WI 53706, USA
Janko Gravner
Mathematics Department,
University of California,
Davis, CA 95616, USA
Abstract
In this simple model for a one-dimensional array of excitable cells, each site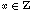 
is in one of 
states: 0 (rested state), 1 (excited state), 
(refractory states). The states update in discrete time according to a synchronous rule: changes 
happen automatically, while the 
change is induced by at least a threshold number of 1s in the local neighborhood of 
. If indestructible stable periodic objects exist, the model evolves into a locally periodic state. In parameter ranges when these structures are impossible, the system approaches the ground state 0: either the dynamics are dominated by annihilating waves, which cause power-law decay, or excitation is unable to propagate and the model experiences exponentially fast relaxation.
